Challenges 7-12: Implementing and breaking AES ECB

Over the recent Christmas break, I picked up the Cryptopals challenges again. After a four-year hiatus, I finally sat down to give the AES implementation another go, only to realize that I had misread the purpose of the challenge and was making it so much harder for myself.

After reading the challenges correctly, I managed to make progress despite family and toddler interruptions. For this set of challenges, I feel I had more issues trying to use Span<byte> than the challenges themselves.

This group of challenges focuses on AES ECB (Electronic Code Book), implementing CBC (Cipher Block Chaining) yourself, and decrypting an AES ECB ciphertext with a padding oracle.

Challenge 7 - AES in ECB mode

This is the challenge that put me off of Cryptopals for a good four years, all because I missed the instruction:

Easiest way: use OpenSSL::Cipher and give it AES-128-ECB as the cipher.

- Cryptopals challenge 7.

I had spent a load of time trying to manually implement AES in C# when it wasn’t actually necessary for the challenge – they were happy for me to use an existing implementation as long as I called it via code. Unsurprisingly, trying to implement AES myself put me off these challenges for a long time. If being put off for four years isn’t a good indication of why you shouldn’t roll your own crypto implementation, I don’t know what is.

For this challenge, I used .NET’s System.Security.Cryptography implementation. I found the setup below to be the best at disabling all of the library’s safety features and allowing me to shoot myself in the foot enough to complete the challenges.

byte[] key;	// must be 16 bytes long
byte[] data;

var aes = Aes.Create();
aes.Key = key;  // symmetric keys
aes.BlockSize = 128; // block size in bits (AES-128)

var ciphertext = aes.EncryptEcb(data, PaddingMode.None);
var plaintext = aes.DecryptEcb(ciphertext, PaddingMode.None);

For this challenge, you do not have to handle irregularly sized data (data that is not an even multiple of the block size). That comes later.

Challenge 8 - Detect AES in ECB mode

Next up is detecting a ciphertext that has been encrypted using ECB.

Remember that the problem with ECB is that it is stateless and deterministic; the same 16 byte plaintext block will always produce the same 16 byte ciphertext.

- Cryptopals challenge 8.

This is the giveaway here. You’re looking for the ciphertext that has a repeating 16-bytes.

There’s not too much to talk about with this one. This challenge gives you a collection of hex strings, and you need to search for repeating blocks (your block size is 128 bits or 16 bytes, which means you can even look for a repeating 32 characters in the hex string). Spoiler: only one of them has repeating blocks.

You may have heard of the ECB penguin. This is where an image (the Linux mascot in this example) is encrypted using AES-ECB. However, because the image contains many repeated blocks, so will the resulting ciphertext. This means that even though you’ve encrypted the image, you can still see the penguin!

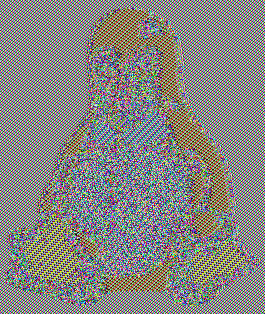
Challenge 9 - Implement PKCS#7 padding

Again, a relatively simple challenge, where you need to append a special character to the end of some plaintext to make the plaintext length an even multiple of the block size.

Be careful not to fall into the same trap that I did and overcomplicate this one. Your pad function needs to know the block size and pad the end of the data appropriately, and your unpad function simply needs to strip all padding characters from the end of the data. The index from end operator comes in handy for this one.

Challenge 10 - Implement CBC mode

This is a fun one. This challenge requires you to build upon your ECB implementation to support irregularly sized messages (thanks to the padding function above) and the CBC block cipher mode. In future challenges, you will be attacking ECB and CBC implementations, so understanding CBC is the goal here. Don’t just use .NET’s CBC implementation this time around.

When encrypting with CBC mode, you XOR your first plaintext block against an Initialization Vector (IV) before passing it to your block cipher encryption function. The next plaintext block is then XORed against the previous ciphertext block. This ensures that a plaintext block always results in a different ciphertext.

I actually found the following diagrams from Wikipedia’s AES explanation to be the most useful:

Here’s an example implementation for CBC encryption, using the AES instance configured above. Check out my full custom AES wrapper for decryption.

const int blockSize = 16; // AES-128
Span<byte> plaintext; // bytes to encrypt
Span<byte> iv; // initialization vector


var ciphertext = new List<byte>();
byte[] previousEncryptedBlock = null;
for (var i = 0; i < plaintext.Length / blockSize; i++)
{
    var blockToEncrypt = plaintext.Slice(i * blockSize, blockSize);
    Span<byte> currentIv;

    if (i == 0)
    {
        // first block XORed against initialization vector
        currentIv = iv;
    }
    else
    {
        // otherwise XORed against previous ciphertext block
        currentIv = previousEncryptedBlock;
    }

    // XOR then encrypt
    byte[] bytesToEncrypt = Xor.ByteArrays(blockToEncrypt, currentIv); // XOR function from challenge 2
    byte[] encryptedBlock = aes.EncryptEcb(Pkcs7.Pad(bytesToEncrypt, blockSize), PaddingMode.None); // PKCS7 implementation from challenge 7 only last block would be padded

    ciphertext.AddRange(encryptedBlock);
    previousEncryptedBlock = encryptedBlock;
}

return ciphertext.ToArray();

After a bit of back-and-forth, hacking around with .NET’s AES implementation, I definitely had a decent dopamine rush after getting this one working!

Unfortunately, this challenge does include a super gate-keepy comment about how you should learn, which sucks. Ignore them and learn and test your solution in whatever way you want. Everyone is different and that’s the way it should be.

Challenge 11 - ECB/CBC detection oracle

Another relatively simple one that involves creating an encryption oracle that randomly uses ECB or CBC. The challenge is to detect whether ECB or CBC was used based on the resulting ciphertext.

Since you can pass the oracle a known plaintext, you can influence the resulting ciphertext. For example, if you pass in plaintext that contains repeating bytes, ECB mode will produce a ciphertext that contains repeating blocks, whereas CBC will not.

Challenge 12 – Byte-at-a-time ECB decryption (simple)

This challenge is a bit more complex, combining everything from the previous challenges.

This time, your encryption oracle will append your plaintext with a value known only to the oracle and then encrypt it using the same key each time. Internally, the oracle uses the following pseudocode, where unknown-value and random-key are constant values known only to the oracle.

AES-128-ECB(your-string || unknown-string, random-key)

The goal of this challenge is to decrypt the unknown-value that is always appended to your plaintext before encryption.

But first, the challenge wants us to make a couple of checks to confirm the block size and block cipher mode. To check the block size, you can call the oracle with an increasingly large plaintext until the resulting ciphertext increases in length. The difference in length will be your block size. For the block cipher mode, you can use the ECB detection functionality from challenge 11.

Once you have confirmed that you are dealing with AES-128-ECB, you can start brute-forcing the unknown plaintext by repeatedly calling the encryption oracle.

Let’s think back to the hint in challenge 8.

Remember that the problem with ECB is that it is stateless and deterministic; the same 16 byte plaintext block will always produce the same 16 byte ciphertext.

- Cryptopals challenge 8.

You can use this to your advantage. You control the data that will be prepended to the secret plaintext known by the oracle, and you know that AES-ECB will always return the same ciphertext block for the same plaintext block.

Combine these facts by passing in just enough known data to isolate a single byte of the unknown value, getting the resulting ciphertext, and then brute-force the oracle to generate the same ciphertext. You can brute force one byte at a time!

First, create a known value – for example, 15 bytes of zero. If you pass this into the encryption oracle, you now know that the last byte of the first block will be a single byte of the unknown value (examples use hexidecimal).

000000000000000000000000000000?? -> fe558ec329f1d59e780be525037f87e8

Now that you know the ciphertext that byte would create, you can start brute forcing it. You can do this by repeatedly calling the encryption oracle with your known bytes and your guessed byte in the last position of the first block.

00000000000000000000000000000000 -> d7026924ef35f9df71f1a5478e5a2085
00000000000000000000000000000001 -> 0de6cc83dc78b132b9256cfed4b5ce59
00000000000000000000000000000002 -> ed9e84971398f984daf36633c72d4b34
...

// ✅ it's a match!
00000000000000000000000000000052 -> fe558ec329f1d59e780be525037f87e8

Once you generate a ciphertext that matches, it means you have discovered the first byte of the unknown value.

Next, you need to isolate the second byte. You can do this by passing a known value that is one byte shorter than the one you used previously. This means that the second byte of the unknown value with be the last byte of the first block.

0000000000000000000000000000???? -> 5de2a24c0ce34d2cfc564de8b89e9d6d

Since you’ve already brute-forced the first byte of the unknown value, you can now brute-force the second byte.

00000000000000000000000000005200 -> 46382d5db9f0f55b7c0b4d94f0ee3d74
00000000000000000000000000005201 -> 45f83c63ae0eacfaa46923d28913b5aa
...

// ✅ it's a match! 
0000000000000000000000000000526f -> 5de2a24c0ce34d2cfc564de8b89e9d6d

Repeat this for the first block until you have decrypted the first block of the unknown value.

You’ll need to apply the same attack to the second block. To isolate the bytes of the next block, you’ll need to apply the same principle, isolating a single byte of the second block, generating a ciphertext, and then using your known values to brute force the single byte.

000000000000000000000000000000?? ????????????????????????????????

Here, you are again passing in the initial 15 known bytes; however, since you already know the first 16 bytes of the unknown value, you know what the oracle was using:

00000000000000000000000000000052 6f6c6c696e2720696e206d7920352e??

This means you can start brute-forcing the first byte of the unknown value’s second block. And then repeat for each subsequent byte and block. Don’t forget to handle the padding!

This is the challenge where I stopped caring about allocations and regretted ever introducing Span into my codebase.

Chosen prefix attack

I did a bit of digging into this attack. While the challenge authors gave some anecdotal evidence that they managed to apply this attack in the wild around once a year, I couldn’t quite understand what use case a system would have to implement this kind of encryption (appending a secret value after arbitrary user input).

You can find a lot of information about chosen plaintext attacks, which is a more general term for this kind of attack. I sometimes saw this referred to as a “chosen prefix attack”, but that doesn’t seem as widespread, nor do many sources state where this kind of attack has succeeded.

Maybe it’s one to chalk up to odd developer choices!